Performance at International Benchmarks

TIMSS Advanced 2015 International Benchmarks of Advanced Mathematics Achievement

As a way of interpreting the scaled achievement results, three points on the advanced mathematics achievement scale were identified as international benchmarks—Advanced (625), High (550), and Intermediate (475). The TIMSS & PIRLS International Study Center worked with the TIMSS 2015 Science and Mathematics Item Review Committee (SMIRC) to conduct a detailed scale anchoring analysis to describe mathematics achievement at the benchmarks and to select example items to illustrate the mathematics content and types of cognitive processing skills and strategies demonstrated by students at each of the international benchmarks. For the items designated for use in reporting the results, every effort was made to include examples that not only illustrated the particular benchmark under consideration, but also represented different item formats and content area domains.

• Advanced Mathematics

download

• pdf
• xls

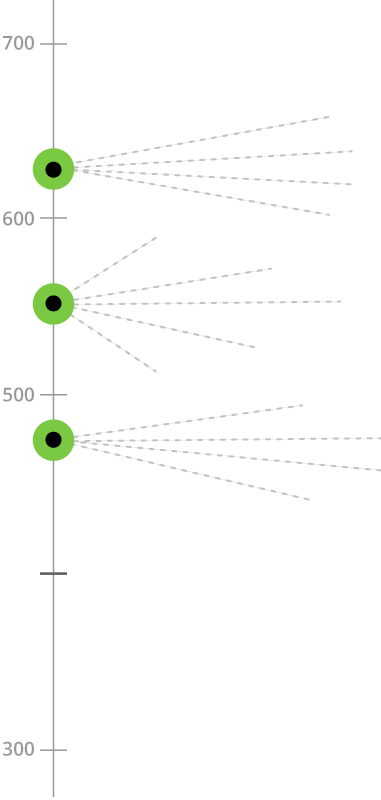
Item Map

INTERNATIONAL BENCHMARKS

Advanced International Benchmark (625)

Advanced International Benchmark (625)
Students demonstrate thorough understanding of concepts, mastery of procedures, and mathematical reasoning skills. They can solve problems in complex contexts in algebra, calculus, geometry, and trigonometry.
More about this benchmark >

High International Benchmark (550)

High International Benchmark (550)
Students can apply a broad range of mathematical concepts and procedures in algebra, calculus, geometry, and trigonometry to analyze and solve multi-step problems set in routine and non-routine contexts.
More about this benchmark >

Intermediate International Benchmark (475)

Intermediate International Benchmark (475)
Students demonstrate basic knowledge of concepts and procedures in algebra, calculus, and geometry to solve routine problems.
More about this benchmark >

EXAMPLE ITEMS

ITEM 1

Example Item 1
Determines the intersection of two functions in terms of an unknown, non-zero coefficient
More about this item >

ITEM 2

Example Item 2
Maximizes the volume of a cylinder given a relationship between its height and diameter
More about this item >

ITEM 3

Example Item 3
Calculates the area between the graphs of a linear and a quadratic function
More about this item >

ITEM 4

Example Item 4
Uses properties of vectors to analyze equivalence of conditions involving the sum and difference of two vectors
More about this item >

ITEM 1

Example Item 1
Determines the values of two constants in a rational expression given its graph with two specified points
More about this item >

ITEM 2

Example Item 2
Solves a word problem involving dimensions of two cylindrical containers given their volumes
More about this item >

ITEM 3

Example Item 3
Identifies the graph of a function given the graph of its first derivative
More about this item >

ITEM 4

Example Item 4
Determines the ratio of the squares of two sides of a scalene triangle given two of its angles
More about this item >

ITEM 5

Example Item 5
Finds the maximum value of a trigonometric function and a value of the independent variable at which it occurs
More about this item >

ITEM 1

Example Item 1
Recognizes the graph of the absolute value of a function given the graph of the function
More about this item >

ITEM 2

Example Item 2
Determines which term has a given value in a geometric sequence
More about this item >

ITEM 3

Example Item 3
Calculates the difference between vectors in coordinate form
More about this item >

ITEM 4

Example Item 4
Solves a word problem about height given the distance and angle of elevation
More about this item >

Summary